本文主要内容系转载。
标准
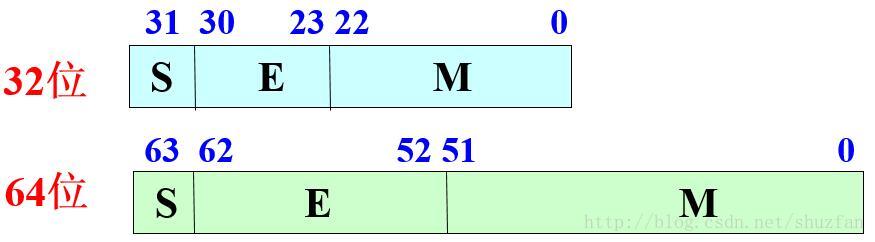
在 IEEE-754 规范[39]中,浮点数由三部分组成:符号位、指数部分和尾数部分(标准化表示方式)。单精度浮点数一般是用 4 字节(32bit)来表示。
不同标准的单精度浮点数、半精度浮点数表示方式[39]
| 数据类型 | 符号位 | 指数部分 | 尾数部分 |
|---|---|---|---|
| FP32 | 1 | 8 | 23 |
| FP16 | 1 | 5 | 10 |
| bFP16 | 1 | 8 | 7 |

规格化表示Normalized
一个浮点数可以有多种表示方式,比如:
1.23 × 102,0.123 × 103,12.3 × 101
为了提高数据的表示精度同时保证数据表示的唯一性,需要对浮点数做规格化处理。
在计算机内,对非0值的浮点数,要求尾数的绝对值必须大于基数的倒数,即|M|≥1R|M|≥1R。
即要求尾数域的最高有效位应为1,称满足这种表示要求的浮点数为规格化表示:把不满足这一表示要求的尾数,变成满足这一要求的尾数的操作过程,叫作浮点数的规格化处理,通过尾数移位和修改阶码实现。
比如,二进制原码的规格化数的表现形式:(0正1负)
正数 0.1xxxxxx
负数 1.1xxxxxx
注意,尾数的最高位始终是1,因此我们完全可以省略掉该位。
至此,我们引入IEEE754 标准,该标准约束了浮点数的大部分使用设置:(尾数用原码;阶码用“移码”;基为2)
(1) 尾数用原码,且隐藏尾数最高位。
原码非0值浮点数的尾数数值最高位必定为 1,因此可以忽略掉该位,这样用同样多的位数就能多存一位二进制数,有利于提高数据表示精度,称这种处理方案使用了隐藏位技术。当然,在取回这样的浮点数到运算器执行运算时,必须先恢复该隐藏位。
(2) 阶码使用“移码”,基固定为2
于是,
一个规格化的32位浮点数x的真值为:
x=(−1)s×(1.M)×2E−127 一个规格化的64位浮点数x的真值为:
x=(−1)s×(1.M)×2E−1023
大端小端
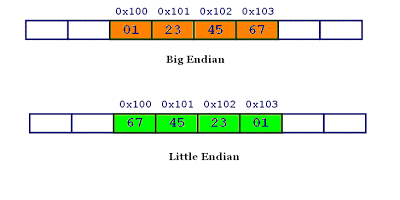
计算机硬件有两种储存数据的方式:大端字节序(big endian)和小端字节序(little endian)。
举例来说,数值0x2211使用两个字节储存:高位字节是0x22,低位字节是0x11。
- 大端字节序:高位字节在前,低位字节在后,这是人类读写数值的方法。
- 小端字节序:低位字节在前,高位字节在后,即以
0x1122形式储存。
0x1234567的大端字节序和小端字节序的写法如下图。
为什么会有小端字节序?
答案是,计算机电路先处理低位字节,效率比较高,因为计算都是从低位开始的。所以,计算机的内部处理都是小端字节序。
但是,人类还是习惯读写大端字节序。所以,除了计算机的内部处理,其他的场合几乎都是大端字节序,比如网络传输和文件储存。
Examples
一个32位单精度浮点数-3.75
(1) 首先转化为2进制表示
−3.75=−(2 + 1 + 1/2 + 1/4)=−1.111×21 (2) 整理符号位并进行规格化表示
−1.111×21=(−1)(1) × (1+0.1110 0000 0000 0000 0000 000)×21
(3) 进行阶码的移码处理 (−1)(1)×(1+0.1110 0000 0000 0000 0000 000)×21 =(−1)(1)×(1+0.1110 0000 0000 0000 0000 000)×2128−127
于是,符号位S=1,尾数M为1110 0000 0000 0000 0000 0001110 0000 0000 0000 0000 000阶码E为12810=1000 00002,则最终的32位单精度浮点数为
1 1110 0000 0000 0000 0000 000 1000 0000
Comments