1. Introduction
本文介绍了半精度浮点数的基本概念以及f32到f16转换的截断法。
混合精度逐渐成为提升深度学习速度的一种有效方法,其本质上,是以运算的精度换速度,当然前提是精度需要在可接受的范围内,或者说应用本身具有容错性(error tolerant)。
在cuda中,half2以及tensorcore的应用,就是对于精度损失容忍性的体现。
2. 半精度浮点数
2.1 位宽
一个float单精度浮点数一般是4bytes(32bit)来表示,由三部分组成:符号位、指数部分(表示2的多少次方)和尾数部分(小数点前面是0,尾数部分只表示小数点后的数字)。
单精度浮点数float的这三部分所占的位宽分别为:1,8,23
半精度浮点数half的这三部分所占的位宽分别为:1,5,10
| Type | Sign | Exponent | Significand field | Total bits | Exponent bias | Bits precision | Number of decimal digits | |
|---|---|---|---|---|---|---|---|---|
| Half (IEEE 754-2008) | 1 | 5 | 10 | 16 | 15 | 11 | ~3.3 | |
| Single | 1 | 8 | 23 | 32 | 127 | 24 | ~7.2 | |
| Double | 1 | 11 | 52 | 64 | 1023 | 53 | ~15.9 | |
| x86 extended precision | 1 | 15 | 64 | 80 | 16383 | 64 | ~19.2 | |
| Quad | 1 | 15 | 112 | 128 | 16383 | 113 | ~34.0 |
2.2 指数部分表示形式
指数部分采用的是偏移指数表示形式(建议参考阅读第 14 章 计算机中数的表示):
| Exponent | Significand = zero | Significand ≠ zero | Equation |
|---|---|---|---|
| 00000~2~ | zero, −0 | subnormal numbers | (−1)^signbit^ × 2^−14^ × 0.significantbits~2~ |
| 00001~2~, ..., 11110~2~ | normalized value | normalized value | (−1)^signbit^ × 2^exponent−15^ × 1.significantbits~2~ |
| 11111~2~ | ±infinity | NaN (quiet, signalling) |
The minimum strictly positive (subnormal) value is 2−24 ≈ 5.96 × 10−8. The minimum positive normal value is 2−14 ≈ 6.10 × 10−5.
2.3 具体表示
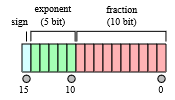
假设内存中有0b 0 10001 00100000
- 第一位为0,表示该数为正数
- 指数位是(10001)~2~ = (17)~10~,所以该数的指数部分是2^17-15^ = 4,
- 尾数部分为(00100000)~2~,补上略去的1即为(1.00100000)~2 ~= (1.1235)~10~
- 所以该数为1.125 * 4 = 4.5
2.4 Half precision examples
These examples are given in bit representation of the floating-point value. This includes the sign bit, (biased) exponent, and significand.
0 01111 0000000000 = 1
0 01111 0000000001 = 1 + 2−10 = 1.0009765625 (next smallest float after 1)
1 10000 0000000000 = −2
0 11110 1111111111 = 65504 (max half precision)
0 00001 0000000000 = 2−14 ≈ 6.10352 × 10−5 (minimum positive normal)
0 00000 1111111111 = 2−14 - 2−24 ≈ 6.09756 × 10−5 (maximum subnormal)
0 00000 0000000001 = 2−24 ≈ 5.96046 × 10−8 (minimum positive subnormal)
0 00000 0000000000 = 0
1 00000 0000000000 = −0
0 11111 0000000000 = infinity
1 11111 0000000000 = −infinity
0 01101 0101010101 = 0.333251953125 ≈ 1/3
3. f32到f16的一种特殊的转换
cuda的ptx中cvt是可以转换f32到f16的,不过如果没有这样的支持,在操作寄存器时,我们可以直接将32位寄存器的高16位mov到新寄存器的高或低16位中。
因为f32前16位中:1位符号、8位指数、7位尾数,再使用该数时,可以使用随机数或者0补全后面丢失的16位尾数。
在转换过程中会丢失精度,结果是否符合要求则根据应用程序不同有不同的标准。
NVidia在2002年提出了半精度浮点数,只使用2个字节16位,包括1位符号、5位指数和10位尾数,能表示的最大数值是 (2−2^−10^) × 2^15^ = 65504, 最小数值2^−14^ ≈ 6.10 × 10^−5^ 。NVidia的方案已经被IEEE-754采纳。
The minimum strictly positive (subnormal) value is 2^−24^ ≈ 5.96 × 10^−8^. The minimum positive normal value is 2^−14^ ≈ 6.10 × 10^−5^
Google的TensorFlow则比较简单粗暴,把单精度的后16位砍掉,也就是1位符号、8位指数和7位尾数。
Comments